Cross Entropy Loss
Cross-Entropy is a widely used loss function, especially in classification tasks, that measures the difference between two probability distributions.
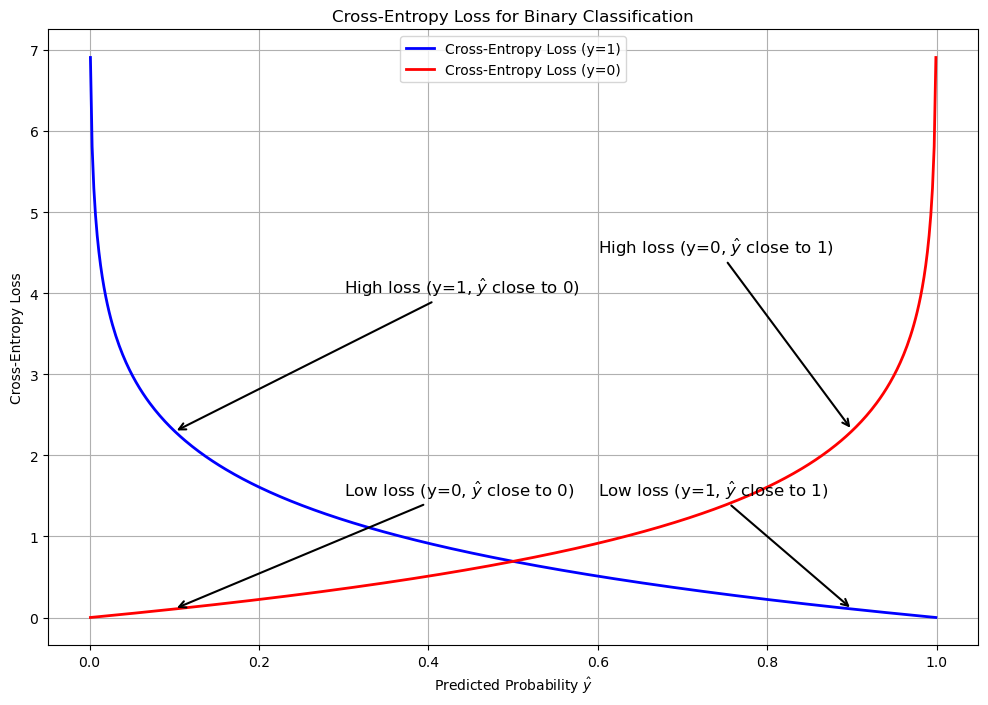
Binary Cross-Entropy (BCE)
2024¶
Gradient Descent Ninja with Momentum
Today, we'll build the gradient descent for a complex function. It's not as easy as it was for the 2D parabola; we need to construct a more complicated method! Momentum - a powerful method to help us solve this challenge!
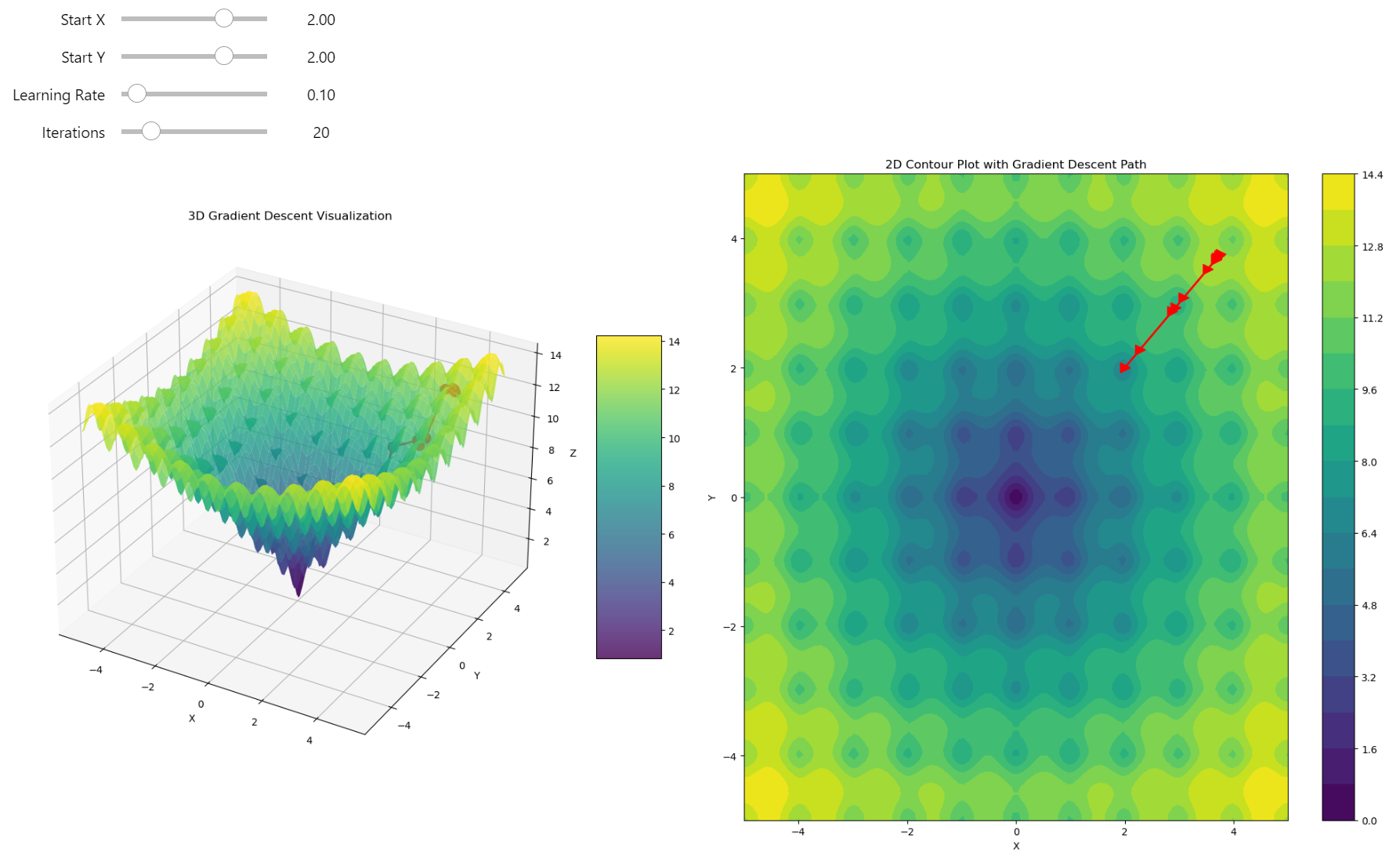
Gradient descent got stuck in a local minimum!
Instability in Numerical Differentiation
Using the Centered Difference approximation of the derivative can lead to numerical instability. Function optimization is a precise task; we cannot afford methods that introduce instability and unpredictability into our results. I've discovered a specific case that illustrates this issue.
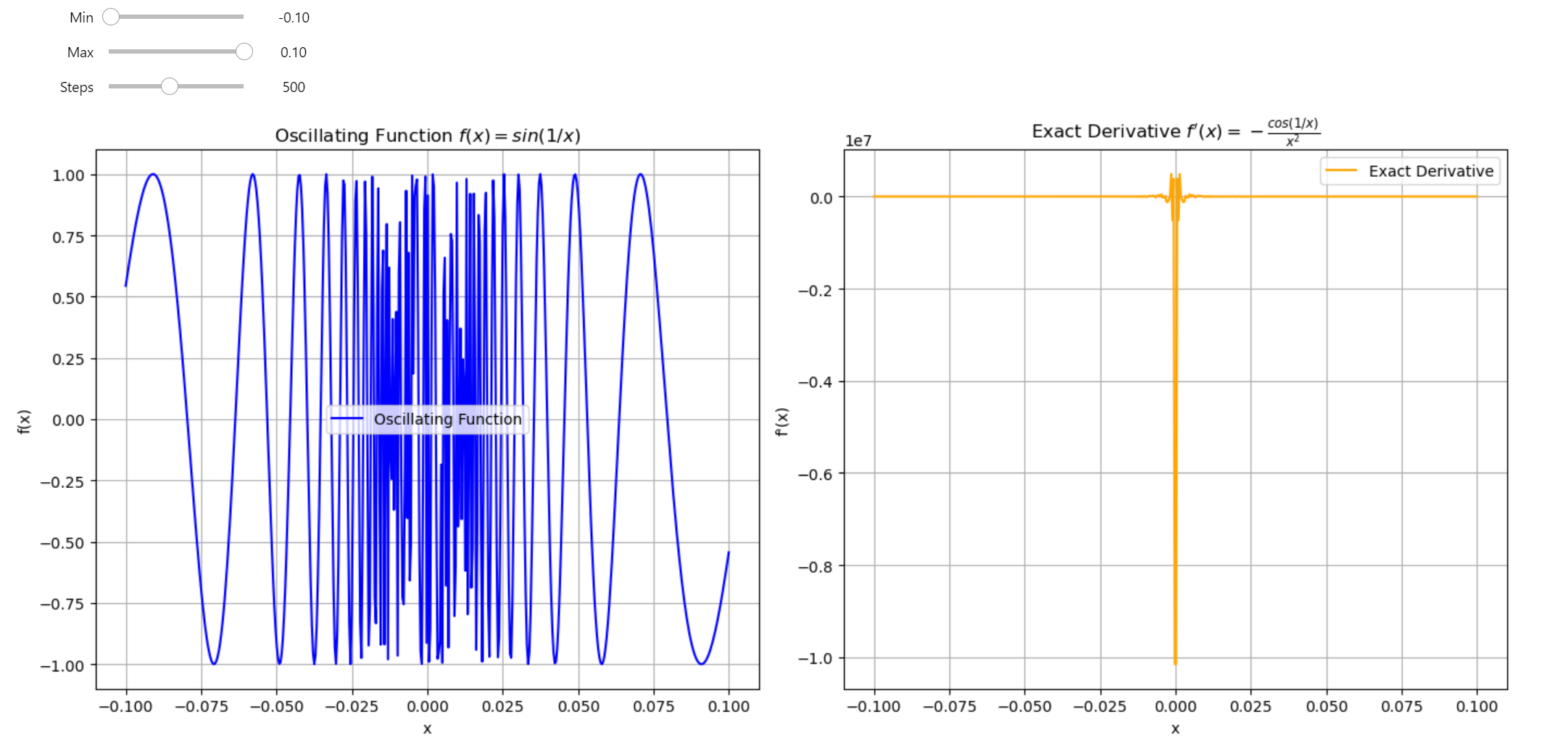
Oscillating Function VS Exact Derivative
Gradient Descent - Downhill to the Minima
The gradient, \( \nabla f(\textbf{x}) \), is a vector of partial derivatives of a function. Each component tells us how fast our function is changing. If you want to optimize a function, you head in the negative gradient direction because the gradient points towards the steepest ascent.
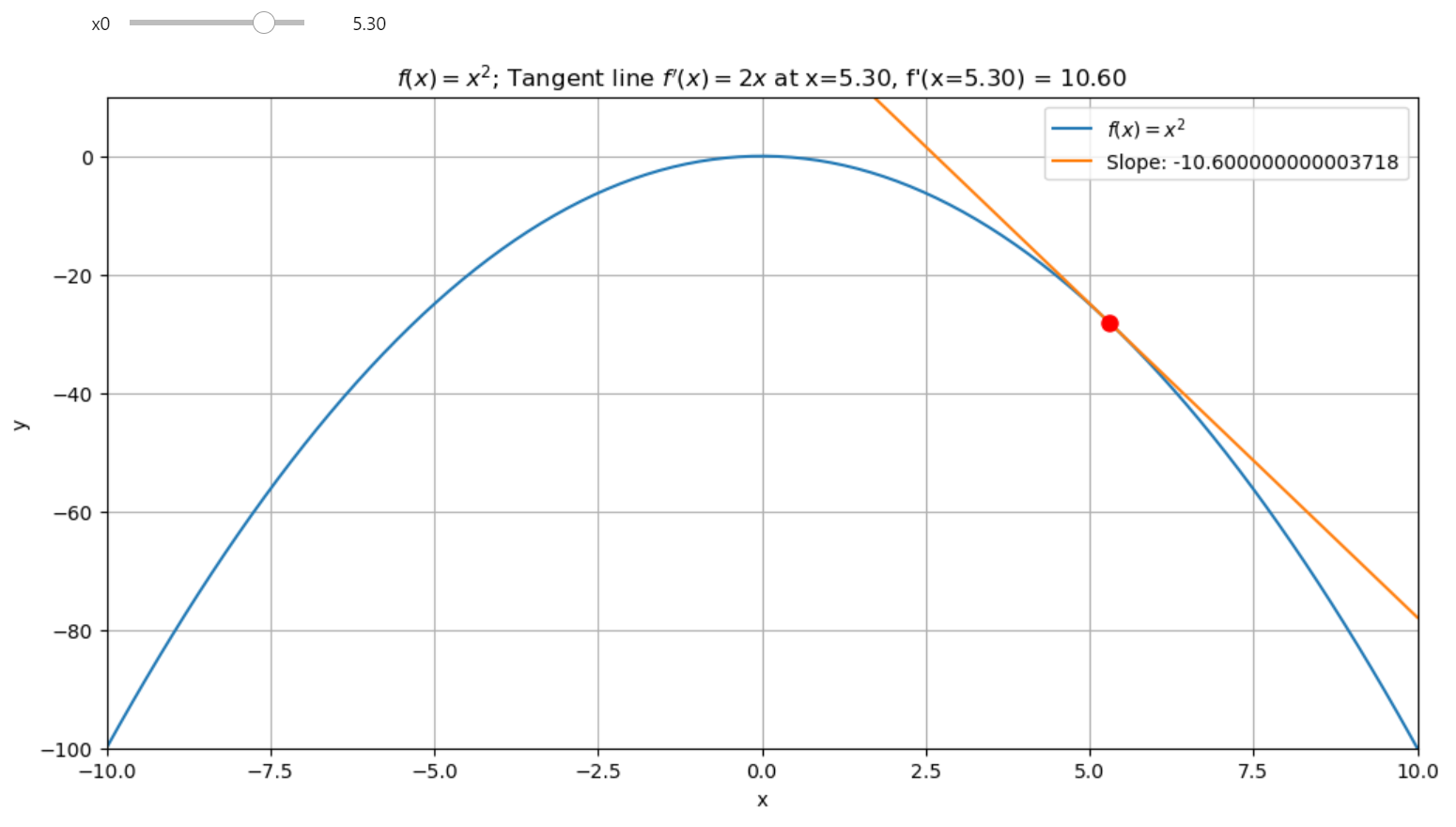
Tangent Line of a function at a given point
Why Does the Gradient Point Upwards?
The gradient, \( \nabla f(\textbf{x}) \), tells us the direction in which a function increases the fastest. But why?
Gradient direction in 3D from Min => Max