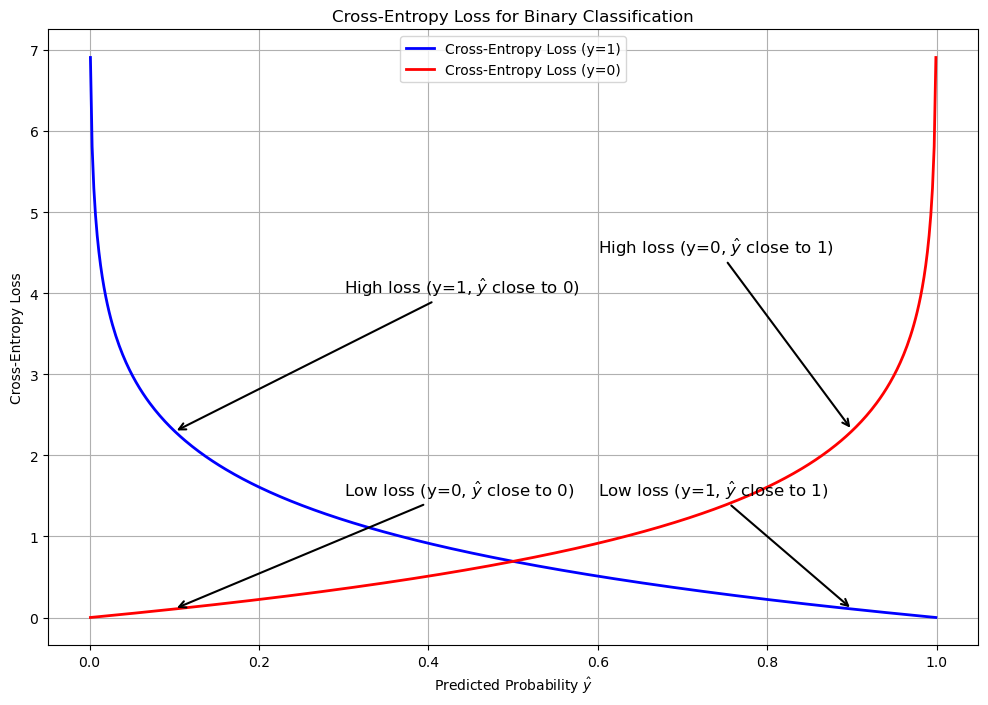
The journey from Logits to Probabilities
Logits are the raw outputs generated by a model before applying any activation function, such as the sigmoid or softmax functions. These values are unbounded, meaning they can be positive, negative, or zero. Logits represent the model's unnormalized confidence scores for assigning an input to different classes.
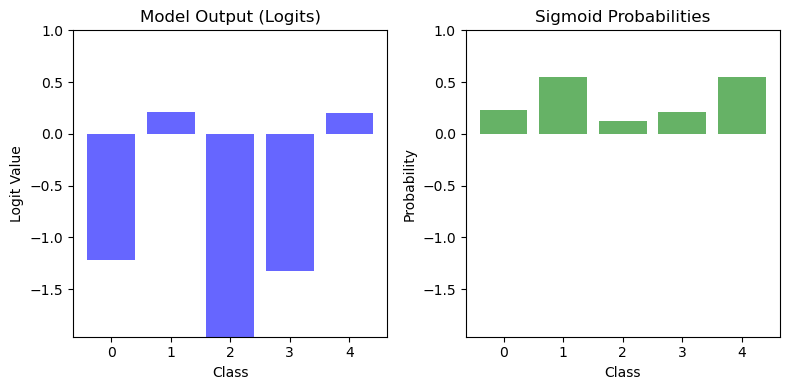
Logits vs Probabilities
In a classification problem, especially in multi-class classification, the model produces a set of logits—one for each class. These logits indicate the model's relative confidence in each class without being normalized into probabilities.